エレベーター問題
みなさんエレベータ好きですか?
私はエレベータに乗ると、人間のあまり良くない部分が見えるのであまり好きでは無いです。 その詳細は本編と全く関係ないので省略するとして、できるだけエレベータに乗っている時間は短くしたいという動機にはつながります。
乗っている時間を短くするためには直通エレベータに乗れば良く、 そうすれば途中で停止することなく、目的とする階数まで最短時間で到着できます。
とはいえ自分のオフィスに直通エレベータなど無いので、その前提で自分のオフィスがある階数まで早く行く方法を考える必要があります。
とにかくはじめます🍛
できるだけ停止させない
エレベータが途中で停止する要因としては2つあり…
- 誰かが途中で降りる
- 誰かが途中で乗ってくる
といっても私は他人が降りたい階数を変えたり、途中で乗ってくる人を制限するような特殊な能力は持っていません。
しかし1.に関しては言えば、最初から自分一人だけが乗るようにすれば回避することは可能です。 とはいえ自分が一人だけになるまで、エレベータに乗らずに待ち続けるとなると、いつまで経ってもオフィスに行けないかもしれません。
そこまでしてオフィスに行く理由はないので帰るという選択肢もありそうですが、ここではもう少し戦略を考えてみます。
エレベータの平均停止回数
どれくらいまで待てばよいのかを知るため、まずはエレベータの平均停止回数を計算してみます。
以下のように定義します。
| 変数 | 意味 |
|---|---|
| F | ビルの最上階 |
| O | オフィスがある階 |
| P | エレベータ内の人(自分以外) |
| S | O階までに止まる回数 |
つまりF階建てのビルにおいて、1階から自分以外のP人と一緒にエレベータに乗った場合、自分のオフィスがあるO階に着くまでに停止する階数はS回となります。
自分はO階に止まるのは確実として、それ以外のP人は2階からF階のどこかに止まる可能性があります。
シミュレーション
実際に以下の仮定に基づきシミュレーションを行いました。
P人の人が止まる回数は完全にランダムで、どの階にも同じ確率で止まる- 誰かが途中で乗ってくることは無い
def sim_stop(person:int, floors:int, office:int):
'''オフィスに着くまでにエレベータが停止する回数を求める'''
getoff = np.random.randint(1, floors, size=person) + 1
stop = len(np.unique(getoff[getoff < office]))
return stop
def sim_stop_N(person:int, floors:int, office:int, iters:int):
'''sim_stopをiters回試行した平均を求める'''
trys = [sim_stop(person, floors, office) for _ in range(iter)]
return np.mean(trys)
def simulation(person:int, floors:int):
'''シミュレーション'''
ret = []
with tqdm(total=person * floors) as pbar:
for p in range(0, person + 1):
for f in range(3, floors + 1):
for o in range(2, f + 1):
s = sim_stop_N(p, f, o, 10000)
ret.append(dict(p=p, f=f, o=o, s=s))
pbar.set_description(f'{p},{f},{o}->{s:.2f}')
pbar.update(1)
return ret
ret = simulation(10, 10)
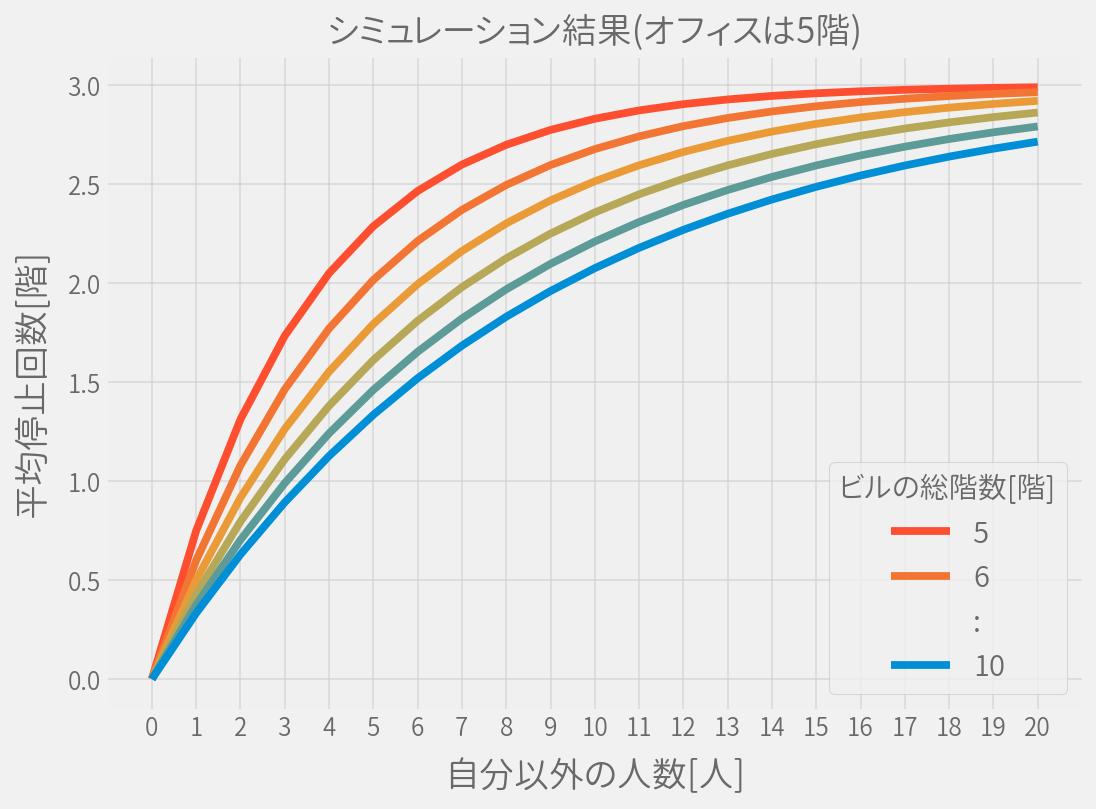
例えば10階建てビルで、オフィスが5階にある場合のシミュレーション結果は以下となりました。
自分だけの場合はP=0なので当然、途中で降りる人はいないため停止回数も0となります。
そして乗る人が増えれば増えるほど、停止回数(S)も上昇していきます。
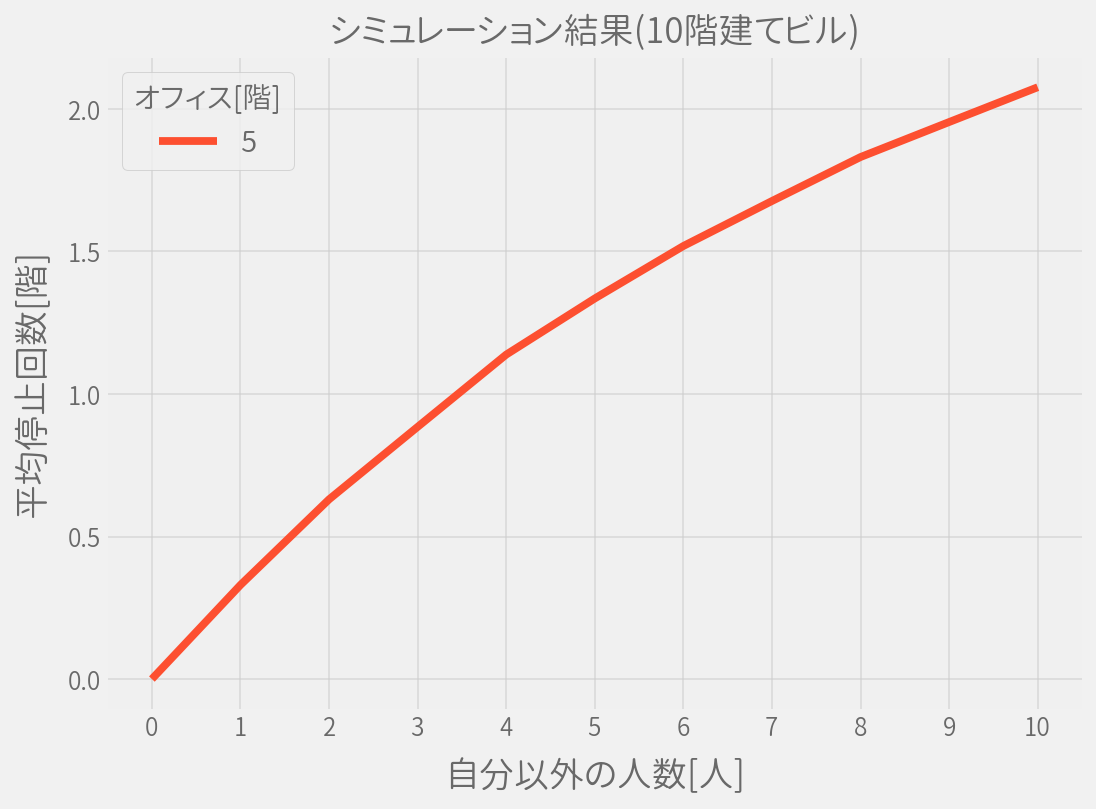
10階建てビルのままオフィスがある階数を2~10階で変化させた場合の結果も見てみます。
いずれも乗っている人(P)が増えれば停止回数も増え、オフィス(O)が上層階にあるほど停止回数(S)に与える影響も多くなります。
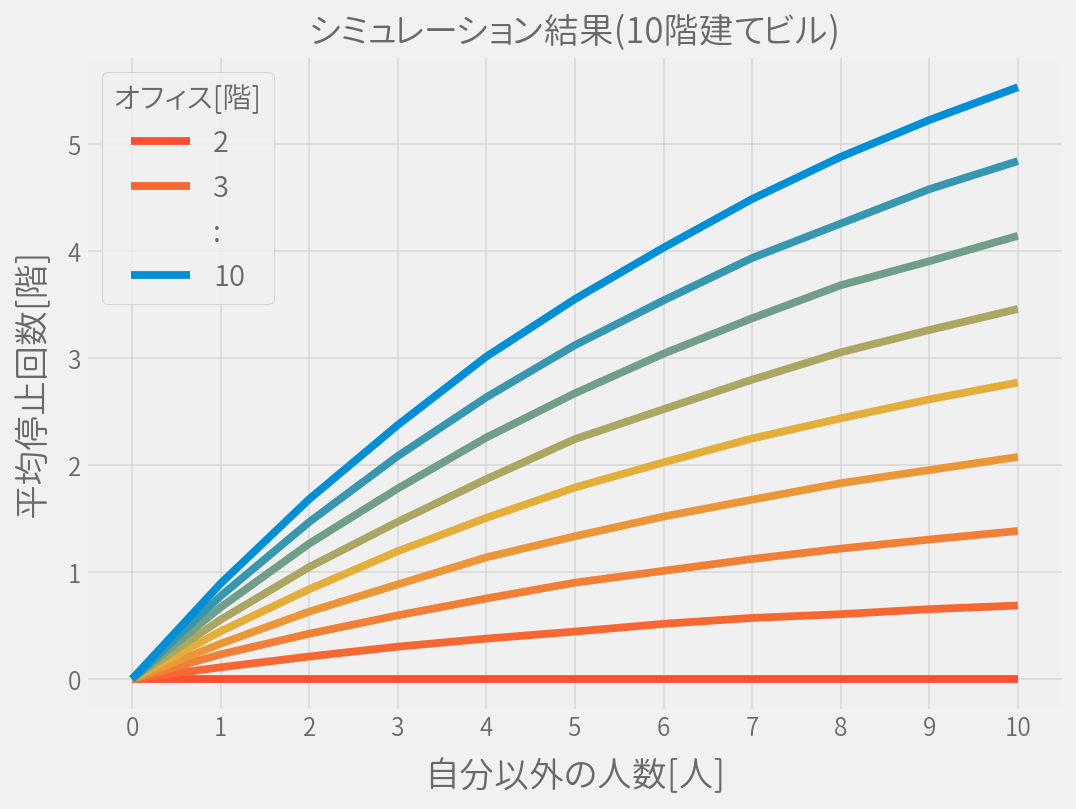
オフィスがある階数を5階に固定して、ビルの高さを変化させると次のようになりました。
ビルが高くなればなるほど、停止回数が少なくなるということです。 ただしその効果はビルが高くなればなるほど小さくなるようです。
だいたい乗っている人(P)が5人以上おり、ビル(F)が5階ほど高くなれば停止回数(S)も1回増えるような感じです。
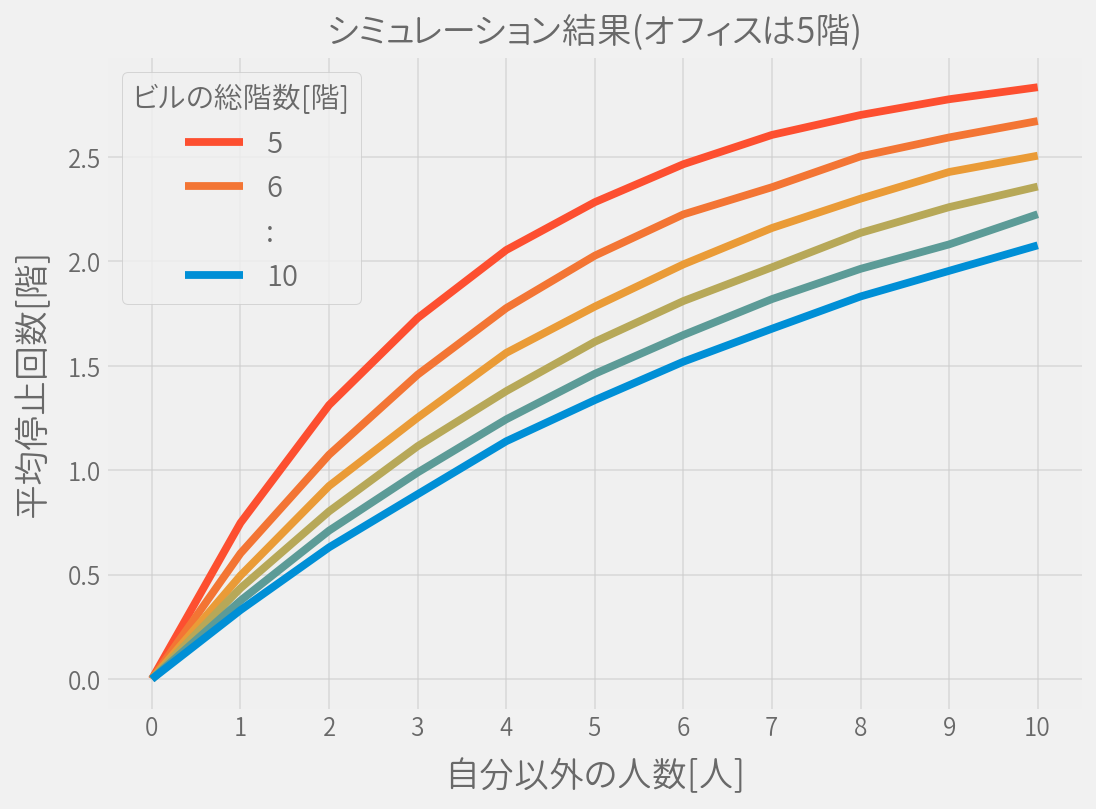
よって出来るだけ高階層のビルでオフィスが低層階にあるほどエレベータの停止回数は少なくなります。 またその場合、自分のオフィスの階層を下げる方がより効果はあります。とはいえ実際問題、自分のオフィスがあるビルを高階層に変える方が難しいでしょうし。
少なくともエレベータ問題に関して言えば、上層階にオフィスがあるメリットは感じません。(だから上層階専用のエレベータなどがあるわけです)
数値計算
シミュレーションが正しいのかを調べるために実際に数値計算もしておきます。
例えば10階建てビルでオフィスが5階にあり、自分以外に3人いる場合、3階に停止する平均回数は次のように考えられます。
(F=10, O=5, P=3)
Pのうち1人が3階に止まる確率:2~10階のいずれかに止まるので1/9Pのうち1人が3階に止まらない確率:1 - 3階に止まる確率 = 8/9Pの全員が3階に止まらない確率:3人の同時確率なので8/9 * 8/9 * 8/9
def calc_stop(person:int, floors:int, office:int):
'''オフィスに着くまでにエレベータが停止する回数を求める'''
return (office - 2) * (1 - (1 - 1 / (floors - 1))**person)
def calculation(person:int, floors:int):
'''数値計算'''
ret = []
with tqdm(total=person * floors) as pbar:
for p in range(0, person + 1):
for f in range(3, floors + 1):
for o in range(2, f + 1):
s = calc_stop(p, f, o)
ret.append(dict(p=p, f=f, o=o, s=s))
pbar.set_description(f'{p},{f},{o}->{s:.2f}')
pbar.update(1)
return ret
ret2 = calculation(20, 10)
というわけでこちらは一瞬で計算が終わるので、シミュレーションと同じグラフにおいて、Pを20人まで増やして描画してみました。
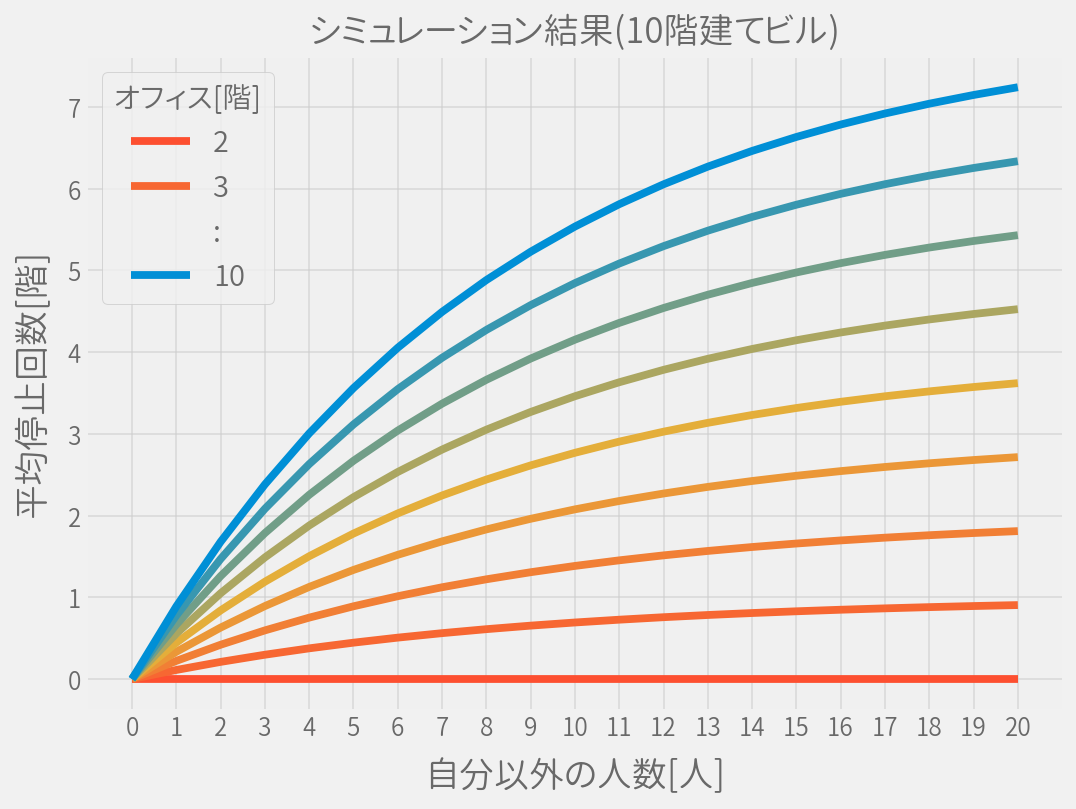
同じくオフィスを5階に固定した場合の結果です。
どうやら同じ結果が得られているようで、シミュレーションが正しかったと言えそうです。(最大の差異は0.04ほどでした)
エレベータ戦略
この結果を受けて私はどのように行動をとるべきでしょうか? 私の場合は以下の環境になります。
F: 10階建てビルO: オフィスは8階
この環境をすぐには変えられないので、変えられる変数は自分以外に乗る人(‘P’)の数です。 よって冒頭で少し述べた戦略に基づき、自分が一人になるよう次のエレベータまで待つという方法を検証してみます。
ただしそのためには情報が不足しているため、ここでは以下のように決めちゃいました。(なんとなく計測した結果に基づく)
| 不足情報 | 値 |
|---|---|
| エレベータの速度 | 1階分の移動に1秒 |
| エレベータ停止時の平均滞在時間 | 5秒 |
| 次のエレベータまでの平均待ち時間 | 20秒 |
この条件でシミュレーションした結果が以下です。
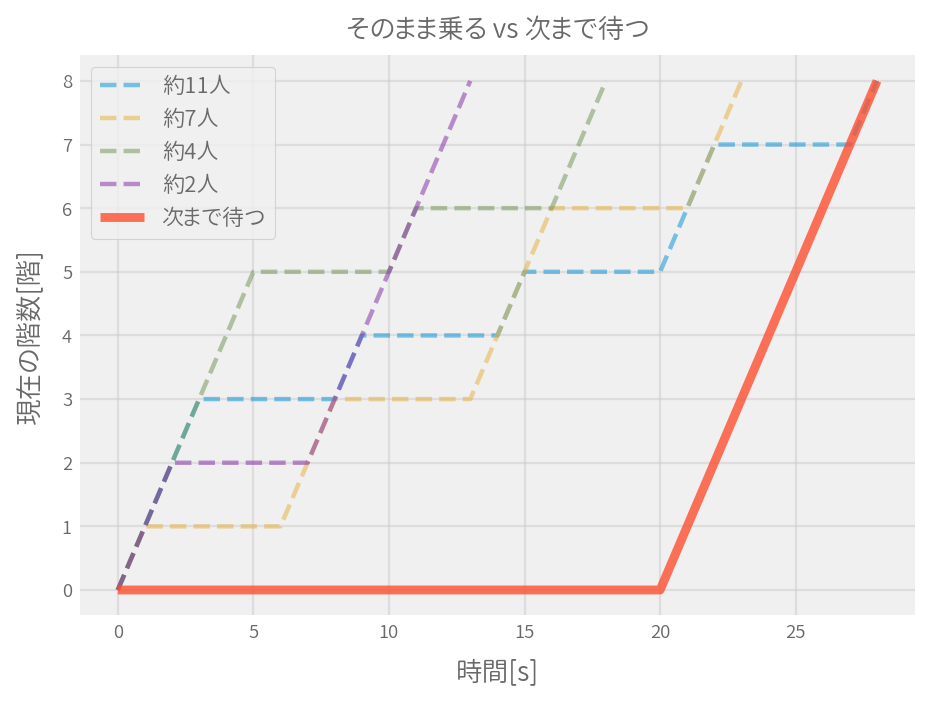
Pが2人ほどなら13秒でオフィスに到着し、Pが11人ほどなら23秒でオフィスに到着するという意味です。
そして次のエレベータまで待った場合も、やはり23秒でオフィスに到着するという結果です。
つまり11人ほど人が居ても、次のエレベータを待ったところでオフィスに到着する時間は変わらないということです。 さらに言えばうちのエレベータはサイズの関係で、11人以上が乗ることはほぼありません。 よって結論としては次のエレベータを待つ必要はなく、そのまま乗れば良いということです。
とにかく私はこれで安心してエレベータを使えます。
まとめ
記事ではもろもろ勝手な仮定を置いてました。
- どの階数にも平等に止まると仮定したが、実際には偏りがある(2階にオフィスがある人はほぼ階段を使うようで2階にはほぼ止まらない)
- 途中で人が乗ってこないと仮定したが、帰宅時やお昼時はこの仮定が当てはまらない
- 次のエレベータまで待てば一人になると仮定したが、実際には待っている間に人はやって来る
これらを考慮して検証することも可能ですが、長くなる(めんどくさい)ので止めておきます。