お買い得な株を定義
- まず直近の財務データに基づき決算時点から半年間の平均株価を予測します。
- 予測された株価より、現在の株価が安ければお買い得と判定します。
ここでいう現在の株価とは、決算発表直後の株価をイメージしています。
つまりある銘柄の予測株価が、現在の平均株価より高い場合、決算日から半年後くらいまでには、その予測株価に近づくはずです。 それが分かってしまえば、簡単に儲けられそうです!
ただお察しの通りこれで儲けることは無理でしょう。
株価が直近の財務データのみで決まるわけでは無いからです。 そもそもそれで決まるなら、株価が日々変動することも無いでしょうし。
ただどこまでできるかやってみます。 なぜならそこから得られる知見が色々ありそうだからです。
とにかくはじめます🍛
とりあえず予測してみましょう
データ分割
まずは学習用とテスト用に分割を行います。
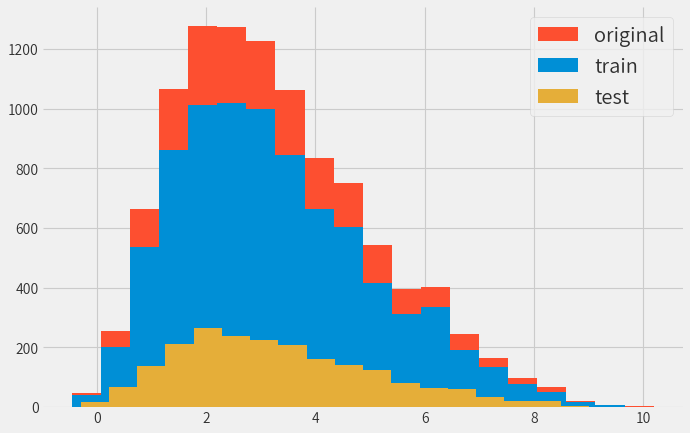
時価総額の割合に応じて、学習データとテストデータを分割したほうが良いかと思いましたが、 ランダムに分割しても結果には大して差が出ませんでした。
参考までに時価総額ベースで分割した結果。
(scikit-learnのStratifiedShuffleSplitを使用)
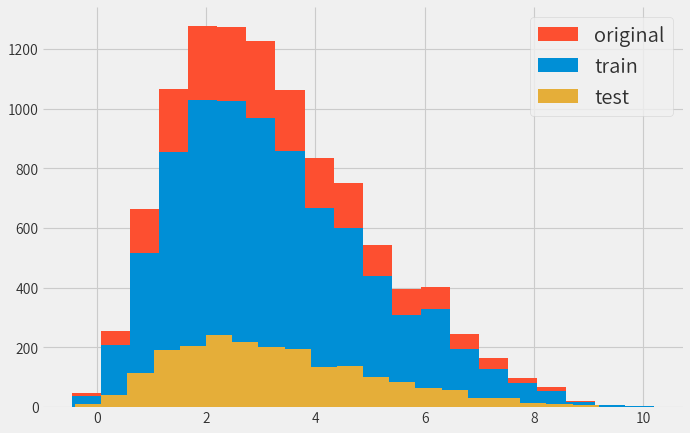
標準化
ここではStandardScalerによる標準化を行い、平均が0で分散が1のデータにしておきます。
前処理にはほかにもいろいろありますが、 詳細はなんやかんやで 公式サイトの解説 が一番わかりやすいのでそちらをご覧ください。
- MinMaxScaler
- MaxAbsScaler
- StandardScaler
- RobustScaler
- Normalizer
- QuantileTransformer
- PowerTransformer
公式以外なら以下も参考になります。
ちなみに結果だけ言えば、どの方法でも予測精度は変わりませんでしたがこれはデータに依存します。
また欠損値についてはとりあえず中央値で補正するようにしておきます。 (平均値を取ると大企業に引っ張られやすいため。)
線形回帰による結果
まずは線形回帰による予測を行います。 この結果は今後の予測モデルの基準にもなるはずです。
なお実際に予測するのは株価ではなく、 株価に発行済み株式数を乗じた時価総額の予測です。 というのも株価より時価総額の方が、財務データとの関連が分かりやすいからです。
つまり今やろうとしていることを改めて言うと、
売り上げなどの財務データ(説明変数)から、半年後の時価総額(目的変数)の予測
です。
当期純利益による回帰(単回帰)
前回の解析では当期純利益と時価総額には相関があることが分かりましたので、まずは説明変数として当期純利益だけを用いた単回帰分析を行います。
model = LinearRegression()
model.fit(x_train.IBITA, y_train)
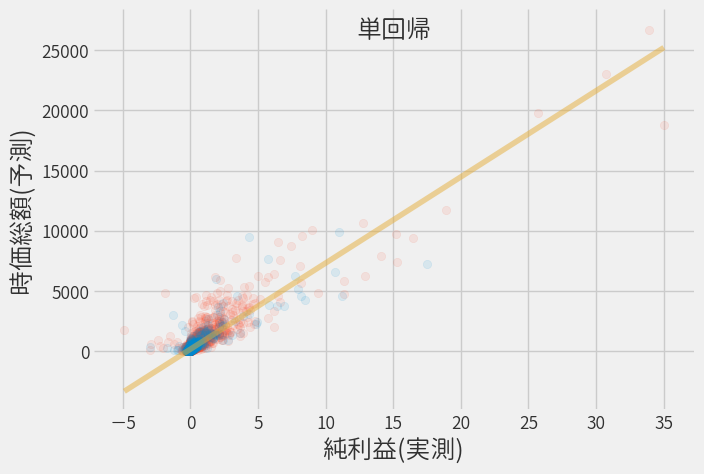
※ 純利益は標準化された値です
視点を少し変えて、実際の時価総額と単回帰による予測結果との差異(残差)をプロットしてみます。
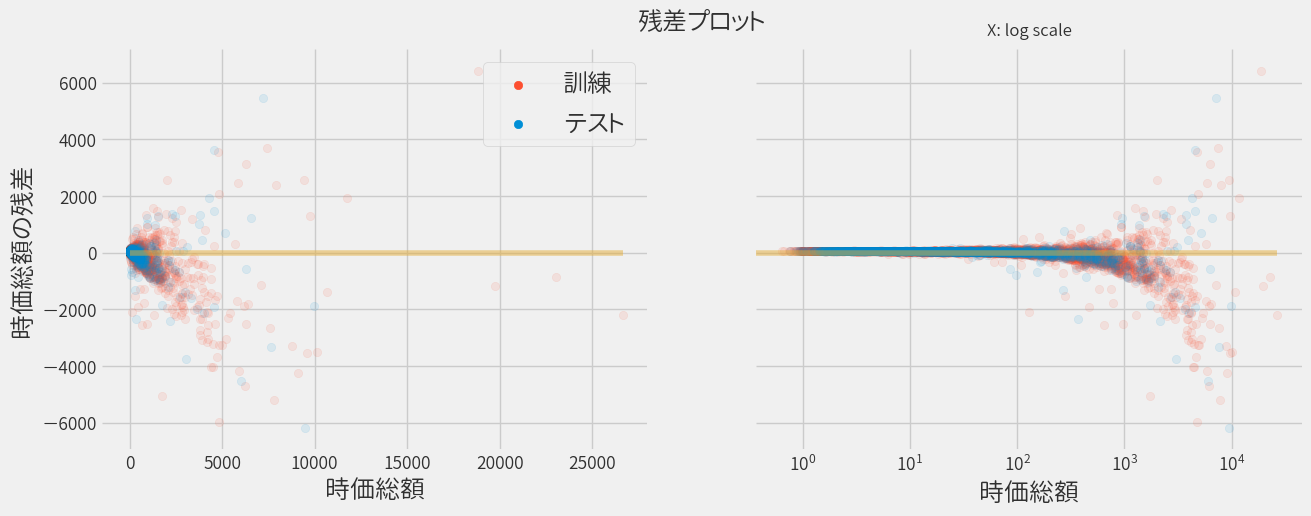
時価総額にバラつきがあるので、ログスケールの図も併せて示しています。
上部の残差がプラスのデータは実際より高く予測された銘柄を意味しており、残差がマイナスのデータは実際より低く予測された銘柄です。 そして残差が0の銘柄は、正しく予測されたことになるので、できる限り0近辺に集まってくれると嬉しい訳です。
ただ時価総額によらず予測精度が均一ならば、時価総額が大きいほど残差の絶対値も大きくなってしまいます。 そこで横軸を株価に直して(発行済み株式数で割る)、再度プロットすると以下のようになります。
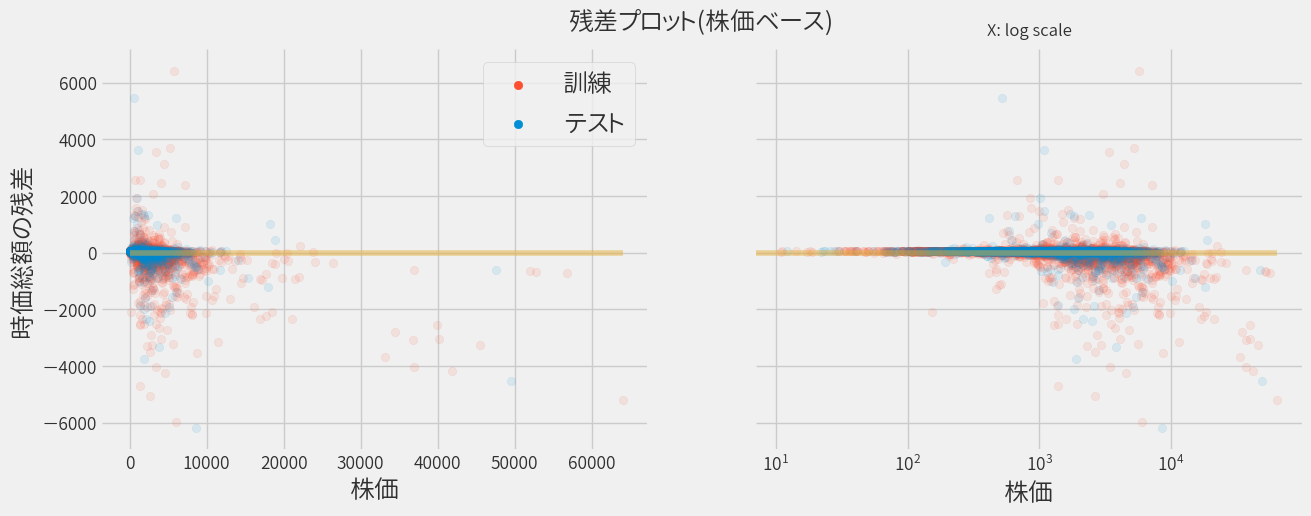
すると全体的にバラつくようになりました。
次に予測モデルの性能を表す指標を示します。
| 対象 | RMSE | R2 |
|---|---|---|
| Train | 320.0(43.0) | 0.80(0.07) |
| Test | 326.0 | 0.72 |
- RMSEは残差の二乗平均平方根誤差、R2は決定係数。いずれも
scikit-learnにより算出 - 数値は交差検証(5分割)による平均値
- 括弧内の数値は交差検証による標準偏差
全項目を用いて予測(重回帰)
次に純利益だけでなく、全項目を用いて回帰分析を行ってみましょう。
model = LinearRegression()
model.fit(x_train, y_train)
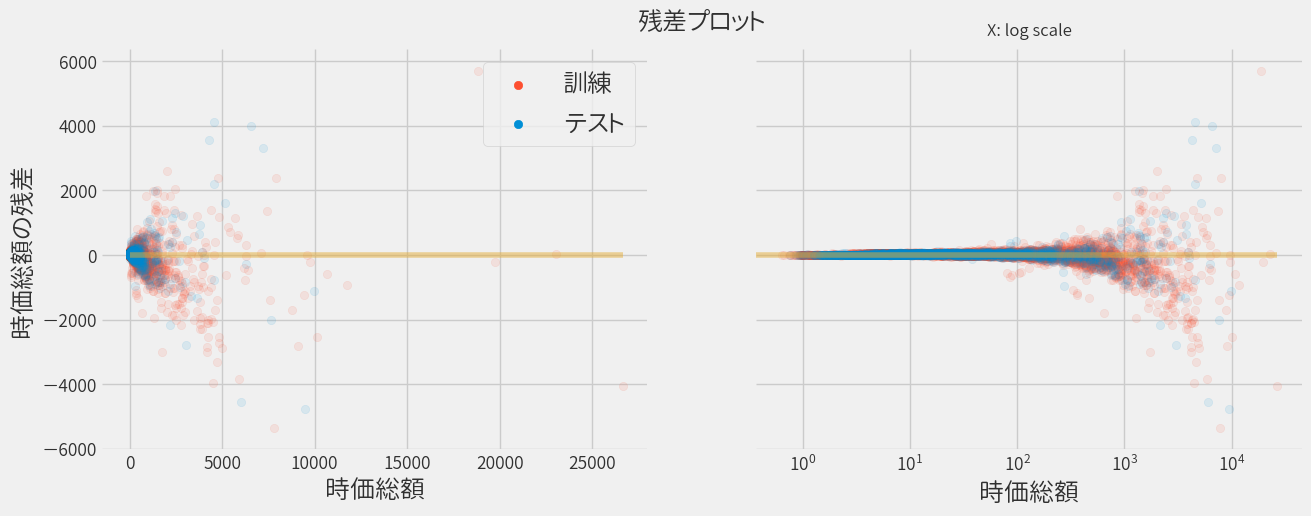
同じく、株価をベースにして再プロットします。
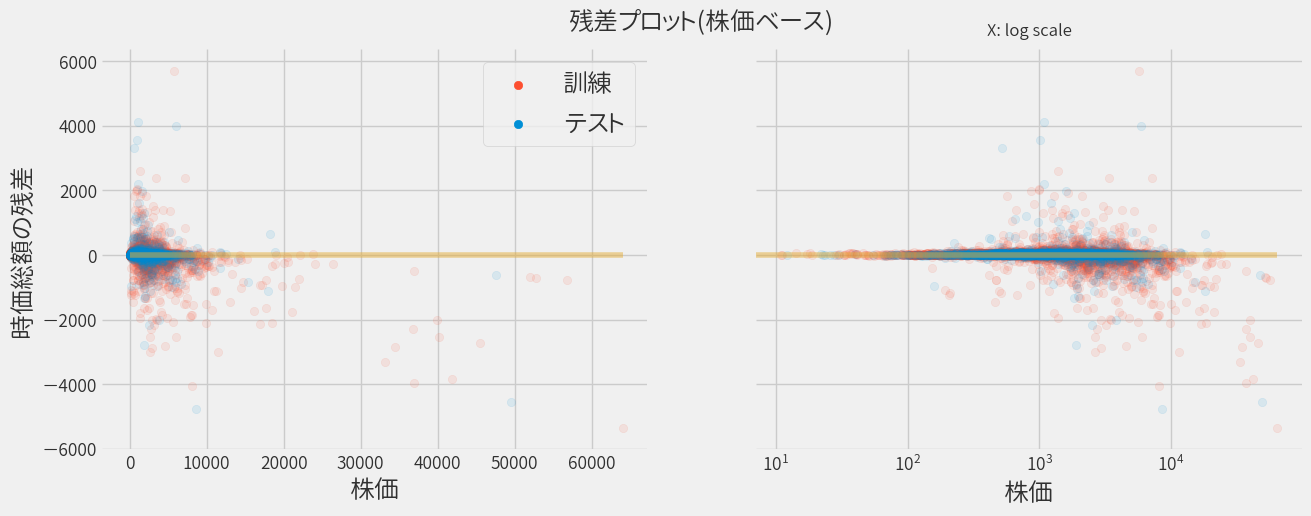
正直なところ先ほどの単回帰の場合と違いが良く分かりませんが、 指標を見ると先ほどよりも良いモデルのようです。
| 対象 | RMSE | R2 |
|---|---|---|
| Train | 304.6(42.3) | 0.82(0.05) |
| Test | 292.4 | 0.78 |
なおscikit-learnで計算される決定係数R2は、いわゆる自由度が調整されていないため単純には比較できません。
ただし今回の場合、自由度で調整しても値の大小は変わらなかったので特に気にしません。 なお自由度調整済みの決定係数の計算は、サンプル数と説明変数の数から簡単に計算できます。1
多項式回帰
これまで結果から項目を増やせば精度が上がるようです。
では 多項式回帰 ならどうなるでしょうか?
scikit-learnではPolynomialFeaturesを用いて変換するだけです。
poly_features = PolynomialFeatures(degree=2, include_bias=False)
x_train_poly = poly_features.fit_transform(x_train)
model = LinearRegression()
model.fit(x_train_poly, y_train)
degree=2にするだけで、30個ほどだった項目数は400個近くになります!
その結果、残差のほとんどが0に集まるようになりました。
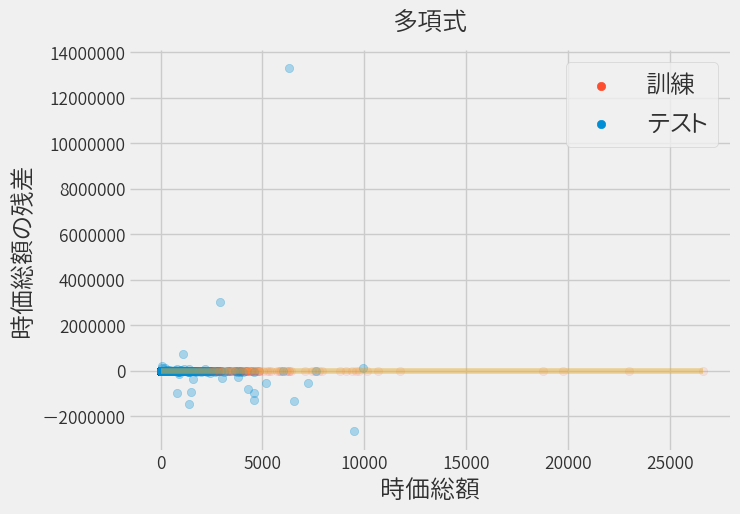
しかし良く見ると集まっているのは学習データのみで、テストデータの予測は大きく外しています。(注:縦軸のスケールが今までより桁違いにでかい)
これを世間では過学習と呼び、指標をみると明らかです。
| 対象 | RMSE | R2 |
|---|---|---|
| Train | 3,4763.0(32728.0) | -7,458.11(13350.15) |
| Test | 31,3190.2.4 | -25,5539.06 |
先に述べたように交差検証をしているため、過学習が発生してもすぐに気づくことができます。
交差検証していない場合
もしトレーニングデータだけで検証していた場合、指標は以下のようになっていました。
単回帰
| 対象 | RMSE | R2 |
|---|---|---|
| Train | 254.3 | 0.894 |
| Test | 292.4 | 0.777 |
学習データに比べてテストデータが多少落ちるのは普通のことです。
多項式回帰
| 対象 | RMSE | R2 |
|---|---|---|
| Train | 95.9 | 0.095 |
| Test | 313,190.2 | -255539 |
こちらは学習データに比べてテストデータは極端にひどいことになっています。
SGD回帰
というわけで単純に項目数を増やすばいい訳ではなく、 学習データに特化することなく汎化性能を上げる必要があります。
SGD回帰を用いて、 学習データの一部を検証データとして用いて、 検証データのRMSEが最小となるようにパラメータをチューニングします。
学習を繰り返すと以下のように学習データと検証データのRMSEはどんどん下がりますが、 検証データに関してはある時点から上昇に転じます。
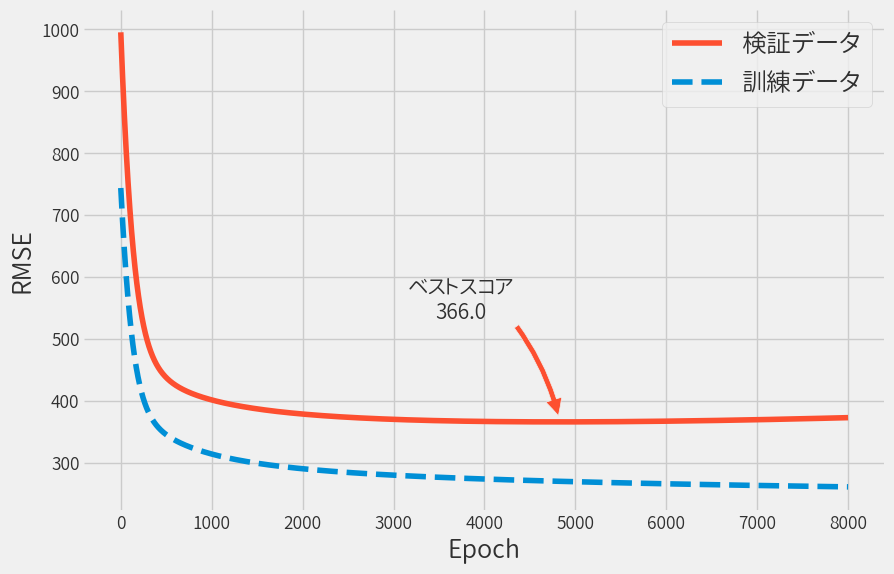
この矢印で示した時点のモデルの性能は以下となりました。
| 対象 | RMSE | R2 |
|---|---|---|
| Train | 320.2(47.8) | 0.80 |
| Test | 323.8 | 0.73 |
残念ながらこのアプローチは思ったほど良くなりませんでした。 とはいえ正則化項や学習率を調整することで、より改善できるかもしれません。
まとめ
線形回帰による予測を行いました。
次回は線形回帰以外の予測モデルにより、さらに予測精度を高めることを目指します。