分割モデルによる対応
予測結果のにいびつさを解消するため、前回は損失関数を変更することで対応を行いました。
ただそもそもの問題として、単独モデルで時価総額が大きく異なるすべての銘柄を表現することに無理があったのかもしれません。
今回は時価総額の大きさに応じた2つのモデルを作成し、それを組み合わせるアプローチを試してみます。 つまり時価総額が大きいモデルに特化したモデルと、時価総額が小さいモデルに特化した2つのモデルとなります。
とにかくはじめます🍛
モデルの分割(LinearRegression)
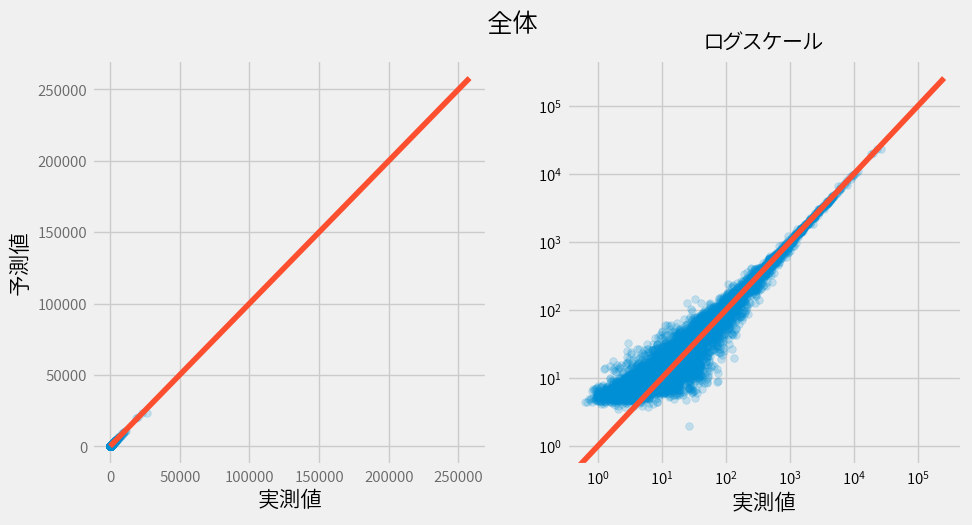
まずは単独モデルでのいびつな結果を載せておきます。
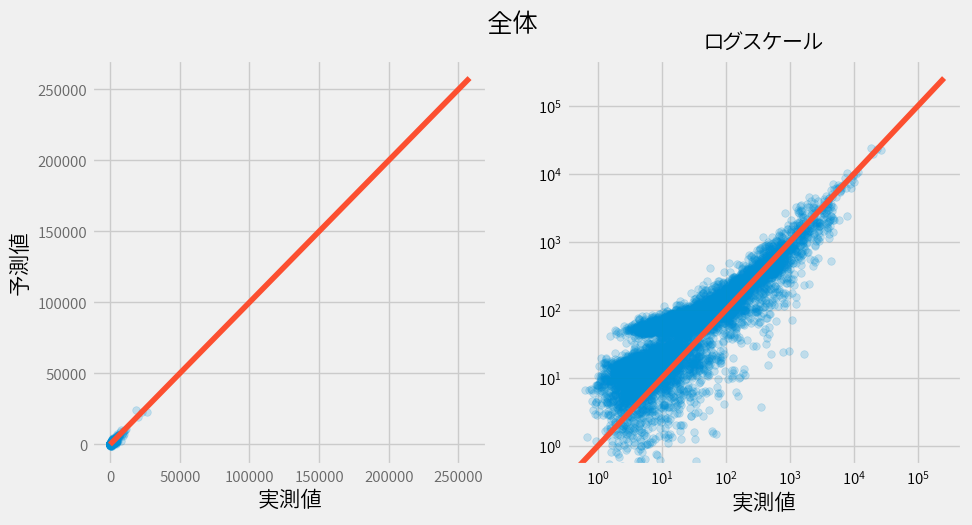
ちなみに精度は以下。見方は今までと同じです。
| 対象 | RMSE | R2 |
|---|---|---|
| Train | 304.6(42.3) | 0.82(0.01) |
| Test | 292.4 | 0.78 |
1000億未満と1000億以上
とりあえず時価総額が1000億(グラフ上では100)を境にデータを分割し、 それぞれ別のモデル(LinearRegression)を作ってみました。
1000億未満のモデル
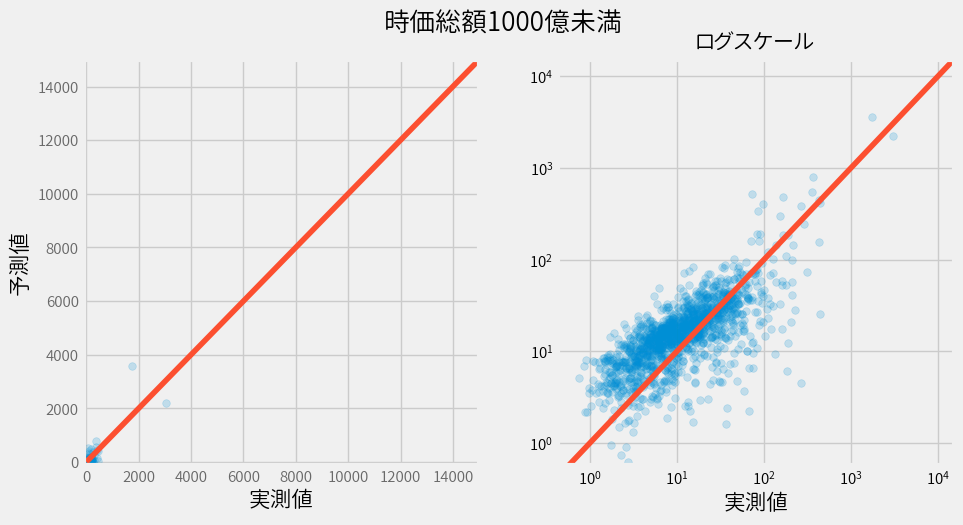
1000億以上のモデル
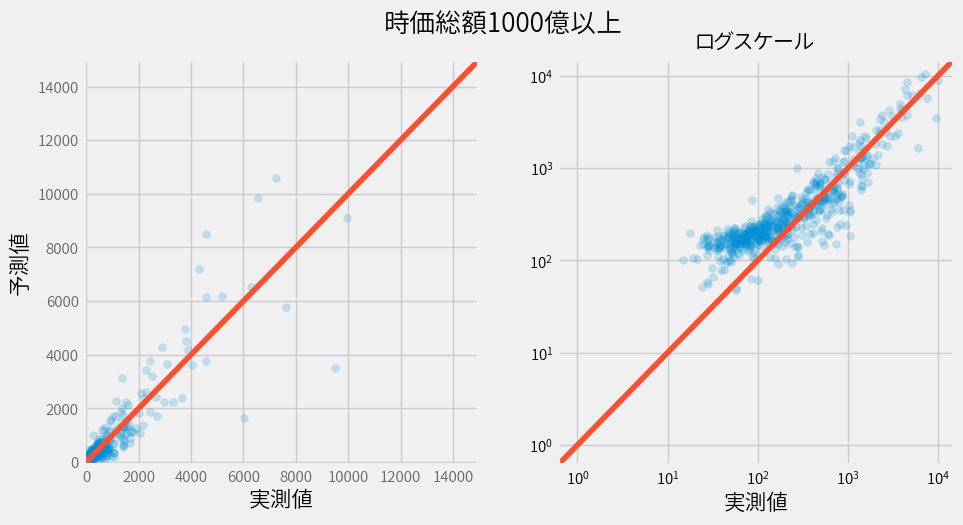
結合
そしてそれぞれのモデルを結合するとこんな感じです。
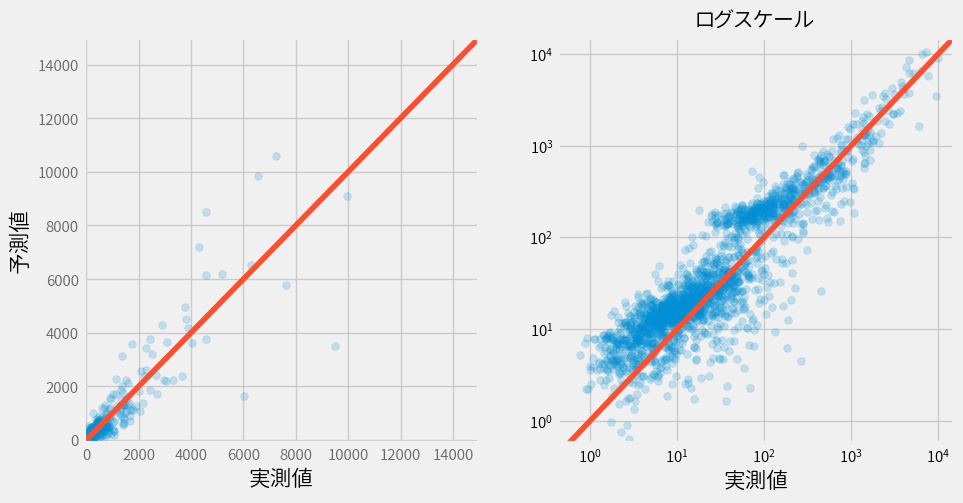
大して綺麗になっていないですね…
精度もほとんど改善されていません。
| 対象 | RMSE | R2 |
|---|---|---|
| Train | 304.4(38.4) | 0.82(0.05) |
| Test | 286.0 | 0.79 |
モデルの分割(XGBRegressor)
より精度の高いXGBRegressorを使用して、もう少し頑張ってみましょう。
どこでモデルを分割すべきか?
適当に “1000億で分割する” などバカなことは言わずに、最適な分割点を探してみましょう。
時価総額を0~100までのパーセンタイル点で分割して、それぞれ求めた精度をプロットした結果が以下です。 (本当は時価総額ではなく当期利益で分割しましたが、結果はほぼ同じなのでご容赦ください。)
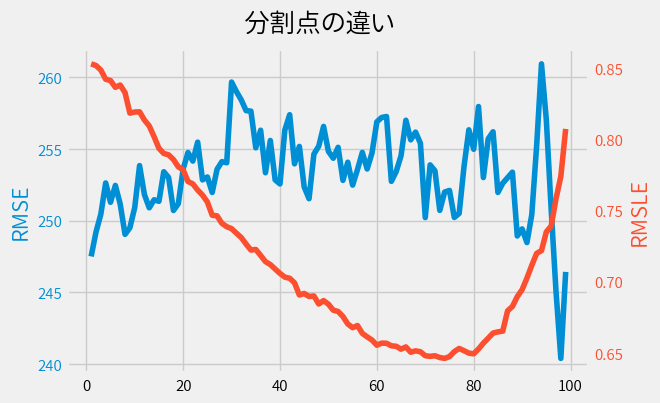
図にはRMSEとRMSELの2つの結果を表示しています。
特徴的なことはパーセンタイル点によりRMSLEも滑らかに変動することです。
一方RMSEにはそのような特性は見られません。
ともかくこの結果74パーセンタイルで分割すると、もっとも精度が高いようです。 74パーセンタイル点は時価総額でいうと765億(グラフ上では76.5)になります。
それではさっそく74パーセンタイル点で分割したモデルの結果を見てましょう。
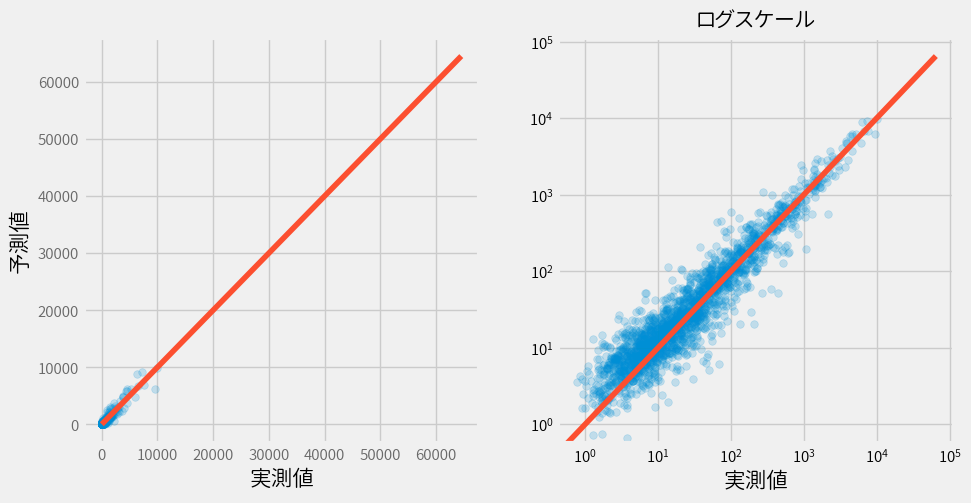
まぁまぁいびつさは改善されました。
なお精度に関して少し触れると、RMSEは183.8から219.2に悪化しました。
しかしRMSLEに関しては0.617から0.570に改善していました。
つまり精度に関してもいびつさはやや改善されたと思われます。
まとめ
というわけでモデル分割によりいびつさを軽減することはできましたが、前回実施した損失関数の変更の方がより効果はあり実装も容易でした。
ただし今回は別のアプローチを取ったにも関わらず、前回登場したRMSLEという指標が判断基準に使えるのは面白いです。
なお今回は2分割でしか試していませんが、別に3つ以上に分割しても良いはずです。やりませんが。
それでは次回、いよいよ割安な株を探すという本来の目的に戻りたいと思います。
が、実はもうやりたいことは(記事にしていないことも含め)だいたい終わったので、割安な株なんてどうでも良くなってたりする…