予測のいびつさ?
まず基準となるLinearRegressionの結果をみてください。
ここで赤い線上は完全に予測できていることを意味しますので、赤い線に予測結果が多く集まっていればいるほど良いモデルです。
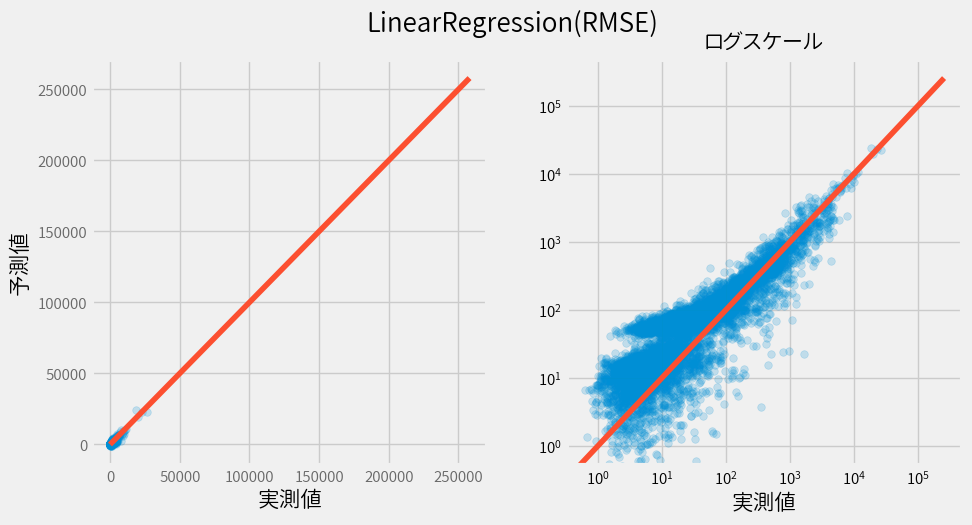
次に前回チューニングを行ったXGBRegressorの結果です。
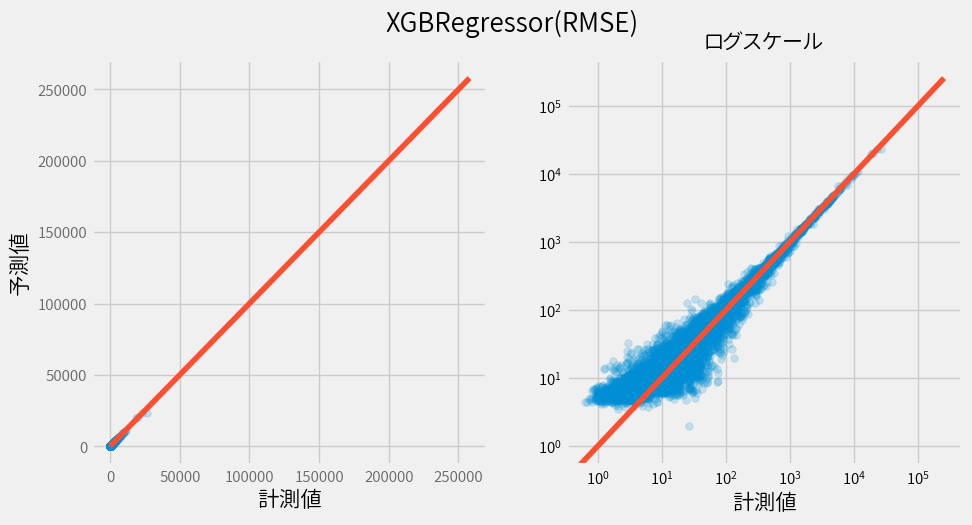
このように可視化するとより分かりやすく精度が上がっていることが確認できます。
ただここで値が小さいほど(グラフの右下)予測値とのずれが大きいことに気づくかと思います。
この原因が損失関数として利用しているRMSE(二乗平均平方根誤差)にありそうなので調べてみましょう。
とにかくはじめます🍛
損失関数による違い
ここまでは損失関数としてRMSEを利用してきましたが、それ以外にも損失関数はたくさん存在します。1
| 略語 | 名称 | 意味 |
|---|---|---|
| MAE | 平均絶対誤差 | 予測差の絶対値の平均 |
| MSE | 平均二乗誤差 | 予測差の二乗値の平均 |
| MSLE | 平均二乗対数誤差 | 対数を取ったMSE |
| MED | 絶対誤差中央値 | 予測差の絶対値の中央値 |
| EV | Explained variance | こちら を参照 |
| R2 | 決定係数 | こちら を参照 |
RMSEはMSEのルートを取って補正したものなので、ほぼ同じです。
例えば以下のように予測1~4がある場合、どの予測が優れているのでしょうか?
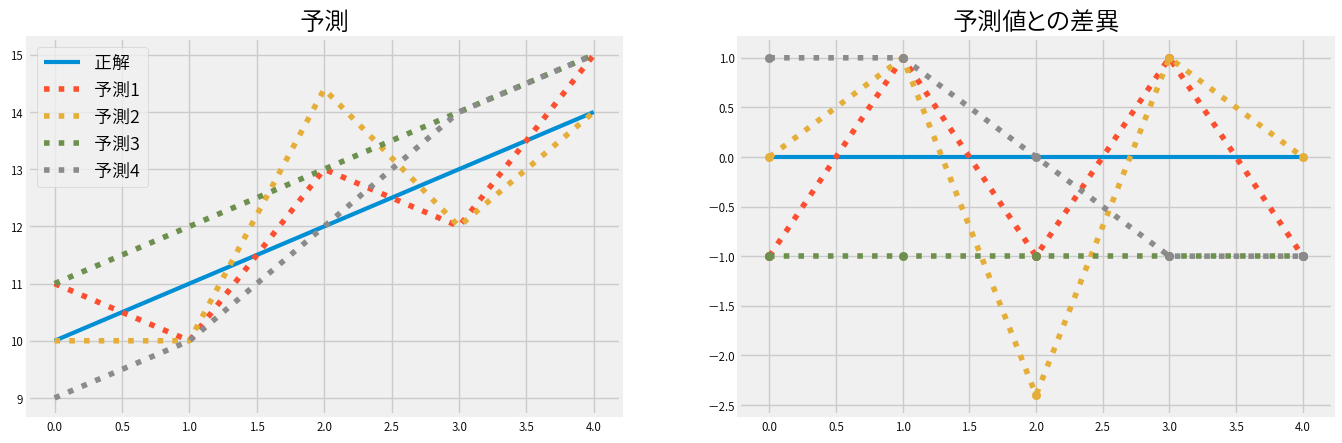
各指標の値を計算すると以下のようになります。
| 予測 | MAE | MSE | MSLE | MED | EV | R2 |
|---|---|---|---|---|---|---|
| 予測1 | 1.00 | 1.00 | 0.0061 | 1.0 | 0.52 | 0.50 |
| 予測2 | 0.88 | 1.55 | 0.0084 | 1.0 | 0.22 | 0.22 |
| 予測3 | 1.00 | 1.00 | 0.0057 | 1.0 | 1.00 | 0.50 |
| 予測4 | 0.80 | 0.80 | 0.0051 | 1.0 | 0.60 | 0.60 |
MAEやMED単独では評価が無理MSE、MSLE、R2を見ると予測4が良く予測2が悪い- 一方で予測1と予測3の優劣は
MSEやR2ではつけられない EV的には予測3が最も良い(予測差異の分散がゼロ)
実は予測3は平行移動すれば正解と一致するので、それを知っていればもっとも実用的です。 しかし単独の指標だけを見ているとそういった事実も見逃してしまうかもしれません。
MSEとMSLEの比較
ここでは特にMSEとMSLEの違いに注目してみます。
次の予測5と予測6はどうでしょうか?
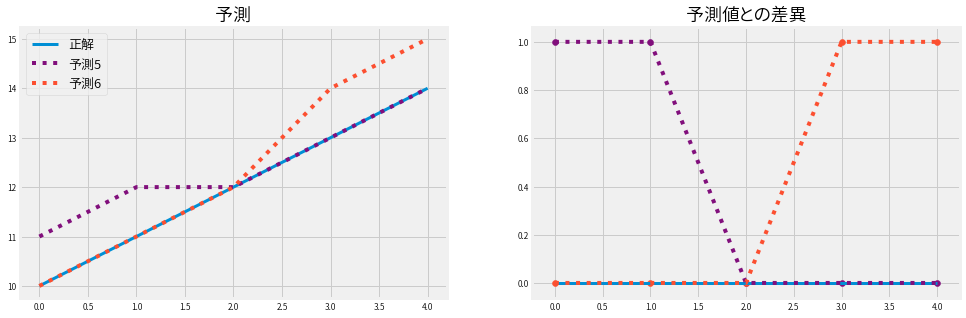
指標としてはMSLE以外はすべて同じです。
| 予測 | MAE | MSE | MSLE | MED | EV | R2 |
|---|---|---|---|---|---|---|
| 予測5 | 0.4 | 0.4 | 0.0028 | 0.0 | 0.88 | 0.8 |
| 予測6 | 0.4 | 0.4 | 0.0018 | 0.0 | 0.88 | 0.8 |
以下の理由でMSLEは値が異なります
MSEは正解との差が1.0であれば、位置に関わらず1.0となります。MSLEは正解との差が1.0でも位置によって値が変わります。
| 横軸位置 | MSE | MSLE |
|---|---|---|
| 1.0の点 | (12-11)^2=1 | (log(12)-log(11))^2=0.0076 |
| 3.0の点 | (14-13)^2=1 | (log(14)-log(13))^2=0.0055 |
言い換えるとlog(12)-log(11)はlog(12/11)なので、
MSLEは差異の割合を見ていることになります。
逆に言うと差異の割合が同じなら、
MSEは値が大きいほどペナルティを大きくしている言えます。
その結果、時価総額が大きい銘柄を最小化するようにモデルが最適化され、予測のいびつさが生じていたと考えられます。
MSLEのうれしい特徴
ついでに以下のような予測3と予測3'(予測3を平行移動)ではどうでしょうか?
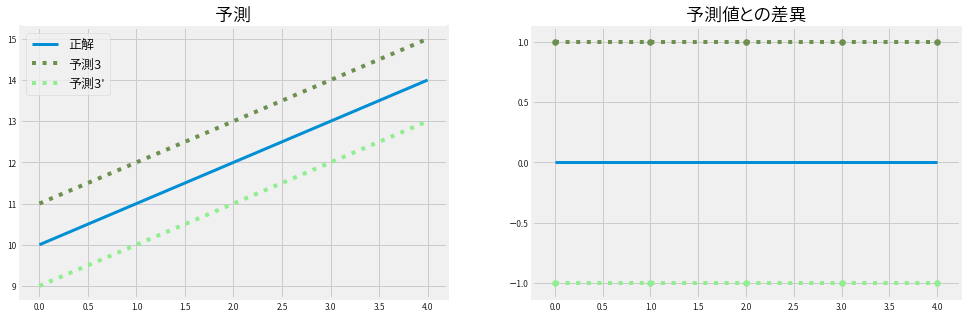
やはりMSLEだけ異なっており、予測3の方が値は小さくなっています。
| 予測 | MAE | MSE | MSLE | MED | EV | R2 |
|---|---|---|---|---|---|---|
| 予測3 | 1.0 | 1.0 | 0.0057 | 1.0 | 1.0 | 0.5 |
| 予測3' | 1.0 | 1.0 | 0.0067 | 1.0 | 1.0 | 0.5 |
つまりMSLEは値が小さいほどペナルティをかけるので、
MSLEで最適化を行うと予測される値は上振れしやすくなります。
これは今回の例でいえば、株価を高めに予測するということになりますが、割安の株を見つけたいのでこの性質は好都合ということです。 (割安と予測する場合は、それだけ自信があるということ)
MSLEにより予測
というわけで今回のモデルにはMSEではなくMSLEが適していることが分かりました。
実際にRMSLE(MSLEのルートを取るだけ)で評価した結果は以下のようになりました。
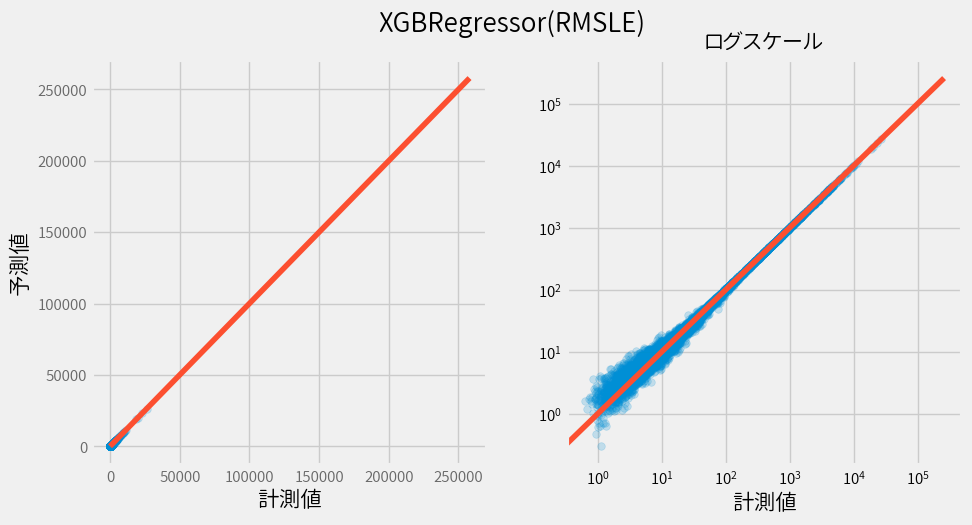
いびつさがかなり解消されました! また結果が上振れしていることも確認できます。
まとめ
通常、回帰問題には二乗平均平方根誤差(RMSE)が使われますが、常にそれが最善ではないことが分かりました。
なお予測結果のいびつさはを解消する方法は他にもありそうです。 例えば、時価総額が小さいグループと大きいグループの2つに分け、 それぞれ別のモデルで予測を行ってみてはどうでしょうか?
次回はそれをやります。