株価(時価総額)の予測

前回は線形回帰モデルとして主にLinearRegressionを利用して株価の予測を行いました。

株で儲けたい-線形回帰により株価を予測してみる | データ駆動はじめ

https://dd1.work/nisa/02_lr/

まずはデータに慣れることを目的に、もっとも基本的な線形回帰を用いて株価(時価総額)を予測してみました。

今回はそれ以外のモデルを適当に選んで、前回同様に株価の予測をしてみました。

とにかくはじめます🍛

SVR(サポートベクトル回帰)

SVRではカーネル関数により非線形モデルに対応することもできます。

sklearn.svm.SVR - scikit-learn 0.21.3 documentation

オプションを指定しない場合、カーネル関数としてRBFが利用されるようです。

model = SVR()
model.fit(x_train, y_train)

結果はこんな感じでボロボロです。

対象	RMSE	R2
Train	710.8(211.1)	0.13(0.05)
Test	563.6	0.17

なお検証方法は前回と同様ですが再掲すると

RMSEは残差の二乗平均平方根誤差、R2は決定係数。いずれもscikit-learnにより算出
交差検証(5分割)による平均値
括弧内の数値は交差検証による標準偏差

デフォルト設定だと全くだったので、 hkaneko1985/fastoptsvrhyperparams の手法を参考にしてハイパーパラメータをチューニングしました。

対象	RMSE	R2
Train	469.7(198.0)	0.63(0.12)
Test	289.2	0.78

改善されましたが、先は長いのでいったんやめましょう。

カーネルリッジ回帰

公式のSVRのページにカーネルリッジ回帰との比較があったので、(記事のタイトルと合わない気もしますが)やっときます。

Comparison of kernel ridge regression and SVR

model = KernelRidge(kernel='rbf', gamma=0.0001)
model.fit(x_train, y_train)

対象	RMSE	R2
Train	341.6 (88.7)	0.79(0.04)
Test	332.1	0.71

gammaをちょっといじったぐらいなのでこんなもんでしょう。

決定木

続いては決定木による回帰を行います。以下のリンク先を見れば、なんとなくやっていることは分かりますね。

Decision Tree Regression - scikit-learn 0.21.3 documentation

model = DecisionTreeRegressor()
model.fit(x_train, y_train)

線形モデルに匹敵する値ですが、過学習気味です。

対象	RMSE	R2
Train	291.4(73.0)	0.83(0.06)
Test	445.4	0.48

もちろんパラメータのチューニングは必要ですが、ここも先を急ぎましょう。

アンサンブル学習

ここからはアンサンブル学習に分類されるモデルを使用します。

なお各モデルのn_estimatorsは10で統一してますが、単純に計算が楽なだけでそれ以上の意味はなしです。

バギング

学習器としてはLinearRegressionを使用します。

全特徴量を利用

10個の学習器の力を集結！

model = BaggingRegressor(
        LinearRegression(),
        n_estimators=10
    )
model.fit(x_train, y_train)

対象	RMSE	R2
Train	345.5(68.5)	0.74(0.19)
Test	334.6	0.71

1個の力より改善せず…

ブートストラップサンプリングされるので、すべてのサンプルが使われるわけでは無い
すべて学習器が同じ特徴量を使用

model.estimators_samples_[0]
# -> array([2010, 1565, 5303, ..., 1434, 3737, 5139])
model.estimators_features_[:3]
# -> [array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30]),
# ->  array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30]),
# ->  array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30])]

アンサンブル学習では個性豊かな学習器の方が精度が良くなるはずです。

特徴量ブートストラップ

というわけで特徴量もブートストラップで選択します。

model = BaggingRegressor(
        LinearRegression(),
        n_estimators=10,
        bootstrap_features=True, # 特徴量もブートストラップ
    )
model.fit(x_train, y_train)

確かに使用される特徴量が変化している

model.estimators_features_[:3]
#-> [array([22,  1,  2, 17, 11, 29, 12, 10, 13,  5, 15, 11, 16, 19, 20,  5,  1, 16, 29, 27,  0, 16,  2, 21,  1, 22, 21, 30,  9, 11, 28]),
#->  array([26, 17, 18,  8,  7,  1, 13, 12, 13, 18, 19, 27,  7, 18,  2, 26,  1, 28, 10, 19,  3,  4, 21, 23, 15, 26, 22,  4, 13, 25,  4]),
#->  array([ 4, 24, 22, 20, 22,  7,  4, 22,  7, 21, 26, 12, 21, 19,  8, 30, 11, 16, 23, 22, 16,  9, 10,  1, 10, 21,  7, 19, 25,  3, 24])]

これでちょっと改善しました。

対象	RMSE	R2
Train	308.7(47.0)	0.79(0.12)
Test	309.6	0.75

ペースティング

ブートストラップサンプリングをしないモデルをペースティングと呼ぶらしいです。

なんにしても実装は簡単で

model = BaggingRegressor(
    LinearRegression(),
    n_estimators=10,
    bootstrap=False, # バギング無効(ペースティング)
    bootstrap_features=True, # 特徴量はブートストラップ
)
model.fit(x_train, y_train)

さらに改善した。

対象	RMSE	R2
Train	287.2(36.8)	0.84(0.05)
Test	288.1	0.78

ここでやっとLinearRegressionを上回った状態です。

ランダムフォレスト

ランダムフォレストもバギングの一種でしょうが、さらに実装が最適化されています。

ちょっとやってみましょう

model = RandomForestRegressor(n_estimators=10)
model.fit(x_train, y_train)

10本(n_estimatorsの数)の木で森と言っていいのか不安でしたが、あっさりとベストスコアが出ました。

対象	RMSE	R2
Train	246.1(63.5)	0.88(0.04)
Test	287.3	0.79

特徴量を制限

ここで各弱学習器で使用される特徴量を制限すると、それぞれの木に多様性が出るはずです。

model = RandomForestRegressor(n_estimators=10, max_features=5)
model.fit(x_train, y_train)

さらなら向上。

対象	RMSE	R2
Train	236.6(78.3)	0.90(0.03)
Test	227.3	0.87

精度は向上しましたが

処理時間は約1/4に短縮した
標準偏差は大きくなった(選択される特徴量によるばらつき)

ExtraTreesRegressor

RandomForestにさらにランダム性を追加したモデルですが、コード上はExtraTreesRegressorに変えるだけです。

# この場合は`max_features`は無くても大して変わらない
# ただし処理時間は短くなるので指定している
model = ExtraTreesRegressor(n_estimators=10, max_features=5)
model.fit(x_train, y_train)

またまたベストスコアを更新。

対象	RMSE	R2
Train	215.2(45.1)	0.91(0.02)
Test	176.3	0.92

ちなみにランダムという要因により処理時間も短くなっています。（処理時間については最後にまとめて表示）

ブースティング

基本的には前の学習器が間違った点を、次の学習器が補填しながら全体としての性能を上げるモデルです。

AdaBoost

弱学習器になにを選ぶかで結果は大きく変わりますが、キリがないのでデフォルトのDecisionTreeRegressorのみで計測します。

model = AdaBoostRegressor(
        DecisionTreeRegressor(max_features=5),
        n_estimators=10,
        learning_rate=0.001)
model.fit(x_train, y_train)

対象	RMSE	R2
Train	238.0(58.9)	0.89(0.04)
Test	184.7	0.91

ちなみに弱学習器にExtraTreeRegressorを使うともっと性能が上がりました、という事実だけお伝えしておきます。㊙️

勾配ブースティング

勾配ブースティングに関してはさすがにn_estimators=10では精度が出ないので、検証データの精度が最も良い木の数を求めました。

検証データとは以下コードの通り、訓練データの一部を使用しています。(テストデータではないです)

x, xv, y, yv = train_test_split(x_train, y_train)
model = GradientBoostingRegressor(max_features=5, n_estimators=500)
model.fit(x, y)
# 検証データ評価
rmse = [np.sqrt(mean_squared_error(yv, p)) for p in model.staged_predict(xv)]
best_n_estimators = np.argmin(rmse)

model = GradientBoostingRegressor(max_features=5, n_estimators=best_n_estimators)
model.fit(x_train, y_train)

訓練データおよび検証データの精度(RMSE)をグラフ化しておきます。

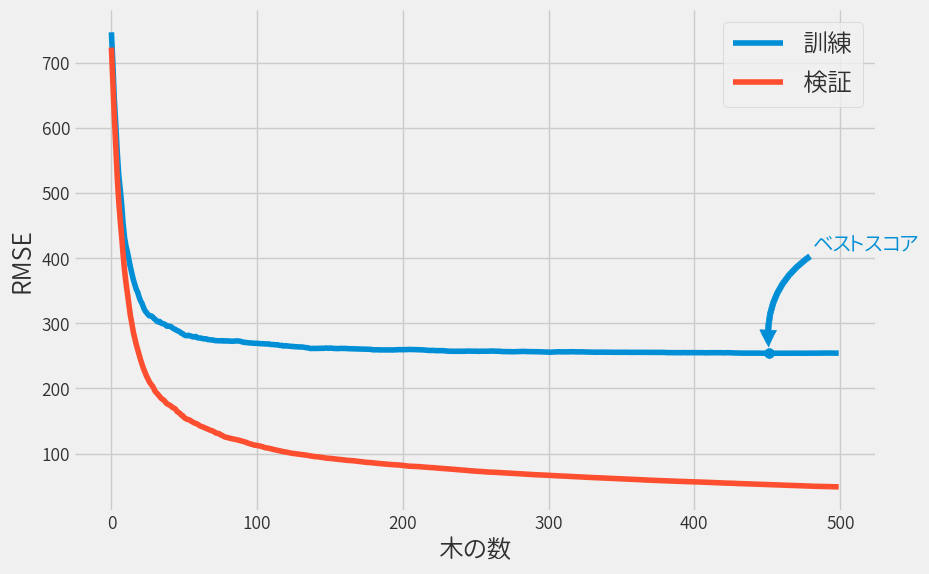
n_estimators以外にもチューニングの余地はあるため、こんなもんでしょうか。

対象	RMSE	R2
Train	216.3(67.3)	0.91(0.03)
Test	198.2	0.90

まとめ

結果をまとめるとこんな感じです。

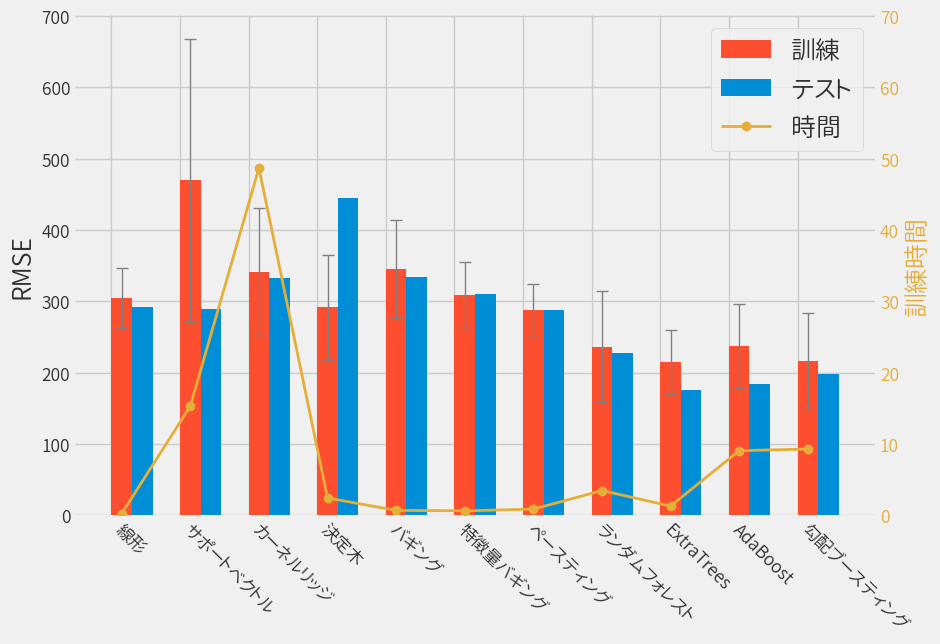
ExtraTreesが良さげという結果になりました。

モデル	RMSE (Train)	RMSE (Test)	訓練時間 [s]
線形	304.6 (42.3)	292.4	0.24
サポートベクトル	469.7 (198.0)	289.2	15.3
カーネルリッジ	341.6 (88.7)	332.1	48.7
決定木	291.4 (73.0)	445.4	2.43
バギング	345.5 (68.5)	334.6	0.69
特徴量バギング	308.7 (47.0)	309.6	0.63
ペースティング	287.2 (36.8)	288.1	0.86
ランダムフォレスト	236.6 (78.3)	227.3	3.47
ExtraTrees	215.2 (45.1)	176.3	1.29
AdaBoost	238.0 (58.9)	184.7	9.06
勾配ブースティング	216.3 (67.3)	198.2	9.29

もちろんこれ以外にも弱学習器の組み合わせで無数にモデルは構築可能です。

もともとは XGboost だけで予測する予定でしたが、その効果を確かめるために色んなモデルを事前に試してみました。

次回はXGboostを使い、さらにハイパーパラメータのチューニングもちゃんとやっていきます。